Gelly: Flink Graph API
Gelly is a Graph API for Flink. It contains a set of methods and utilities which aim to simplify the development of graph analysis applications in Flink. In Gelly, graphs can be transformed and modified using high-level functions similar to the ones provided by the batch processing API. Gelly provides methods to create, transform and modify graphs, as well as a library of graph algorithms.
- Using Gelly
- Graph Representation
- Graph Creation
- Graph Properties
- Graph Transformations
- Graph Mutations
- Neighborhood Methods
- Iterative Graph Processing
- Graph Validation
- Library Methods
Using Gelly
Gelly is currently part of the libraries Maven project. All relevant classes are located in the org.apache.flink.graph package.
Add the following dependency to your pom.xml to use Gelly.
<dependency>
<groupId>org.apache.flink</groupId>
<artifactId>flink-gelly_2.10</artifactId>
<version>1.0.3</version>
</dependency><dependency>
<groupId>org.apache.flink</groupId>
<artifactId>flink-gelly-scala_2.10</artifactId>
<version>1.0.3</version>
</dependency>Note that Gelly is currently not part of the binary distribution. See linking with it for cluster execution here.
The remaining sections provide a description of available methods and present several examples of how to use Gelly and how to mix it with the Flink DataSet API. After reading this guide, you might also want to check the Gelly examples.
Graph Representation
In Gelly, a Graph is represented by a DataSet of vertices and a DataSet of edges.
The Graph nodes are represented by the Vertex type. A Vertex is defined by a unique ID and a value. Vertex IDs should implement the Comparable interface. Vertices without value can be represented by setting the value type to NullValue.
// create a new vertex with a Long ID and a String value
Vertex<Long, String> v = new Vertex<Long, String>(1L, "foo");
// create a new vertex with a Long ID and no value
Vertex<Long, NullValue> v = new Vertex<Long, NullValue>(1L, NullValue.getInstance());// create a new vertex with a Long ID and a String value
val v = new Vertex(1L, "foo")
// create a new vertex with a Long ID and no value
val v = new Vertex(1L, NullValue.getInstance())The graph edges are represented by the Edge type. An Edge is defined by a source ID (the ID of the source Vertex), a target ID (the ID of the target Vertex) and an optional value. The source and target IDs should be of the same type as the Vertex IDs. Edges with no value have a NullValue value type.
Edge<Long, Double> e = new Edge<Long, Double>(1L, 2L, 0.5);
// reverse the source and target of this edge
Edge<Long, Double> reversed = e.reverse();
Double weight = e.getValue(); // weight = 0.5val e = new Edge(1L, 2L, 0.5)
// reverse the source and target of this edge
val reversed = e.reverse
val weight = e.getValue // weight = 0.5Graph Creation
You can create a Graph in the following ways:
- from a
DataSetof edges and an optionalDataSetof vertices:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Vertex<String, Long>> vertices = ...
DataSet<Edge<String, Double>> edges = ...
Graph<String, Long, Double> graph = Graph.fromDataSet(vertices, edges, env);val env = ExecutionEnvironment.getExecutionEnvironment
val vertices: DataSet[Vertex[String, Long]] = ...
val edges: DataSet[Edge[String, Double]] = ...
val graph = Graph.fromDataSet(vertices, edges, env)- from a
DataSetofTuple2representing the edges. Gelly will convert eachTuple2to anEdge, where the first field will be the source ID and the second field will be the target ID. Both vertex and edge values will be set toNullValue.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Tuple2<String, String>> edges = ...
Graph<String, NullValue, NullValue> graph = Graph.fromTuple2DataSet(edges, env);val env = ExecutionEnvironment.getExecutionEnvironment
val edges: DataSet[(String, String)] = ...
val graph = Graph.fromTuple2DataSet(edges, env)- from a
DataSetofTuple3and an optionalDataSetofTuple2. In this case, Gelly will convert eachTuple3to anEdge, where the first field will be the source ID, the second field will be the target ID and the third field will be the edge value. Equivalently, eachTuple2will be converted to aVertex, where the first field will be the vertex ID and the second field will be the vertex value:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Tuple2<String, Long>> vertexTuples = env.readCsvFile("path/to/vertex/input");
DataSet<Tuple3<String, String, Double>> edgeTuples = env.readCsvFile("path/to/edge/input");
Graph<String, Long, Double> graph = Graph.fromTupleDataSet(vertexTuples, edgeTuples, env);-
from a CSV file of Edge data and an optional CSV file of Vertex data. In this case, Gelly will convert each row from the Edge CSV file to an
Edge, where the first field will be the source ID, the second field will be the target ID and the third field (if present) will be the edge value. Equivalently, each row from the optional Vertex CSV file will be converted to aVertex, where the first field will be the vertex ID and the second field (if present) will be the vertex value. In order to get aGraphfrom aGraphCsvReaderone has to specify the types, using one of the following methods: types(Class<K> vertexKey, Class<VV> vertexValue,Class<EV> edgeValue): both vertex and edge values are present.edgeTypes(Class<K> vertexKey, Class<EV> edgeValue): the Graph has edge values, but no vertex values.vertexTypes(Class<K> vertexKey, Class<VV> vertexValue): the Graph has vertex values, but no edge values.keyType(Class<K> vertexKey): the Graph has no vertex values and no edge values.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create a Graph with String Vertex IDs, Long Vertex values and Double Edge values
Graph<String, Long, Double> graph = Graph.fromCsvReader("path/to/vertex/input", "path/to/edge/input", env)
.types(String.class, Long.class, Double.class);
// create a Graph with neither Vertex nor Edge values
Graph<Long, NullValue, NullValue> simpleGraph = Graph.fromCsvReader("path/to/edge/input", env).keyType(Long.class);val env = ExecutionEnvironment.getExecutionEnvironment
val vertexTuples = env.readCsvFile[String, Long]("path/to/vertex/input")
val edgeTuples = env.readCsvFile[String, String, Double]("path/to/edge/input")
val graph = Graph.fromTupleDataSet(vertexTuples, edgeTuples, env)- from a CSV file of Edge data and an optional CSV file of Vertex data.
In this case, Gelly will convert each row from the Edge CSV file to an
Edge. The first field of the each row will be the source ID, the second field will be the target ID and the third field (if present) will be the edge value. If the edges have no associated value, set the edge value type parameter (3rd type argument) toNullValue. You can also specify that the vertices are initialized with a vertex value. If you provide a path to a CSV file viapathVertices, each row of this file will be converted to aVertex. The first field of each row will be the vertex ID and the second field will be the vertex value. If you provide a vertex value initializerMapFunctionvia thevertexValueInitializerparameter, then this function is used to generate the vertex values. The set of vertices will be created automatically from the edges input. If the vertices have no associated value, set the vertex value type parameter (2nd type argument) toNullValue. The vertices will then be automatically created from the edges input with vertex value of typeNullValue.
val env = ExecutionEnvironment.getExecutionEnvironment
// create a Graph with String Vertex IDs, Long Vertex values and Double Edge values
val graph = Graph.fromCsvReader[String, Long, Double](
pathVertices = "path/to/vertex/input",
pathEdges = "path/to/edge/input",
env = env)
// create a Graph with neither Vertex nor Edge values
val simpleGraph = Graph.fromCsvReader[Long, NullValue, NullValue](
pathEdges = "path/to/edge/input",
env = env)
// create a Graph with Double Vertex values generated by a vertex value initializer and no Edge values
val simpleGraph = Graph.fromCsvReader[Long, Double, NullValue](
pathEdges = "path/to/edge/input",
vertexValueInitializer = new MapFunction[Long, Double]() {
def map(id: Long): Double = {
id.toDouble
}
},
env = env)- from a
Collectionof edges and an optionalCollectionof vertices:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
List<Vertex<Long, Long>> vertexList = new ArrayList...
List<Edge<Long, String>> edgeList = new ArrayList...
Graph<Long, Long, String> graph = Graph.fromCollection(vertexList, edgeList, env);If no vertex input is provided during Graph creation, Gelly will automatically produce the Vertex DataSet from the edge input. In this case, the created vertices will have no values. Alternatively, you can provide a MapFunction as an argument to the creation method, in order to initialize the Vertex values:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// initialize the vertex value to be equal to the vertex ID
Graph<Long, Long, String> graph = Graph.fromCollection(edgeList,
new MapFunction<Long, Long>() {
public Long map(Long value) {
return value;
}
}, env);val env = ExecutionEnvironment.getExecutionEnvironment
val vertexList = List(...)
val edgeList = List(...)
val graph = Graph.fromCollection(vertexList, edgeList, env)If no vertex input is provided during Graph creation, Gelly will automatically produce the Vertex DataSet from the edge input. In this case, the created vertices will have no values. Alternatively, you can provide a MapFunction as an argument to the creation method, in order to initialize the Vertex values:
val env = ExecutionEnvironment.getExecutionEnvironment
// initialize the vertex value to be equal to the vertex ID
val graph = Graph.fromCollection(edgeList,
new MapFunction[Long, Long] {
def map(id: Long): Long = id
}, env)Graph Properties
Gelly includes the following methods for retrieving various Graph properties and metrics:
// get the Vertex DataSet
DataSet<Vertex<K, VV>> getVertices()
// get the Edge DataSet
DataSet<Edge<K, EV>> getEdges()
// get the IDs of the vertices as a DataSet
DataSet<K> getVertexIds()
// get the source-target pairs of the edge IDs as a DataSet
DataSet<Tuple2<K, K>> getEdgeIds()
// get a DataSet of <vertex ID, in-degree> pairs for all vertices
DataSet<Tuple2<K, Long>> inDegrees()
// get a DataSet of <vertex ID, out-degree> pairs for all vertices
DataSet<Tuple2<K, Long>> outDegrees()
// get a DataSet of <vertex ID, degree> pairs for all vertices, where degree is the sum of in- and out- degrees
DataSet<Tuple2<K, Long>> getDegrees()
// get the number of vertices
long numberOfVertices()
// get the number of edges
long numberOfEdges()
// get a DataSet of Triplets<srcVertex, trgVertex, edge>
DataSet<Triplet<K, VV, EV>> getTriplets()// get the Vertex DataSet
getVertices: DataSet[Vertex[K, VV]]
// get the Edge DataSet
getEdges: DataSet[Edge[K, EV]]
// get the IDs of the vertices as a DataSet
getVertexIds: DataSet[K]
// get the source-target pairs of the edge IDs as a DataSet
getEdgeIds: DataSet[(K, K)]
// get a DataSet of <vertex ID, in-degree> pairs for all vertices
inDegrees: DataSet[(K, Long)]
// get a DataSet of <vertex ID, out-degree> pairs for all vertices
outDegrees: DataSet[(K, Long)]
// get a DataSet of <vertex ID, degree> pairs for all vertices, where degree is the sum of in- and out- degrees
getDegrees: DataSet[(K, Long)]
// get the number of vertices
numberOfVertices: Long
// get the number of edges
numberOfEdges: Long
// get a DataSet of Triplets<srcVertex, trgVertex, edge>
getTriplets: DataSet[Triplet[K, VV, EV]]Graph Transformations
- Map: Gelly provides specialized methods for applying a map transformation on the vertex values or edge values.
mapVerticesandmapEdgesreturn a newGraph, where the IDs of the vertices (or edges) remain unchanged, while the values are transformed according to the provided user-defined map function. The map functions also allow changing the type of the vertex or edge values.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, Long> graph = Graph.fromDataSet(vertices, edges, env);
// increment each vertex value by one
Graph<Long, Long, Long> updatedGraph = graph.mapVertices(
new MapFunction<Vertex<Long, Long>, Long>() {
public Long map(Vertex<Long, Long> value) {
return value.getValue() + 1;
}
});val env = ExecutionEnvironment.getExecutionEnvironment
val graph = Graph.fromDataSet(vertices, edges, env)
// increment each vertex value by one
val updatedGraph = graph.mapVertices(v => v.getValue + 1)- Filter: A filter transformation applies a user-defined filter function on the vertices or edges of the
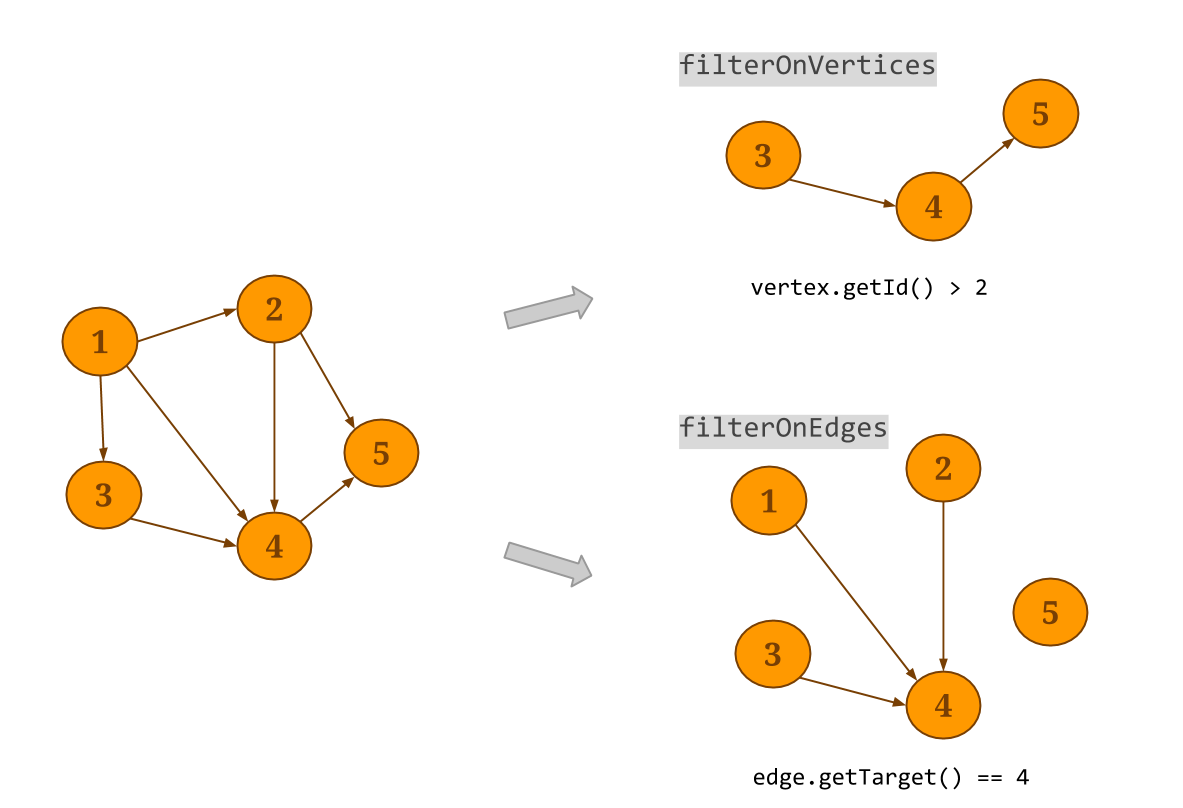
Graph.filterOnEdgeswill create a sub-graph of the original graph, keeping only the edges that satisfy the provided predicate. Note that the vertex dataset will not be modified. Respectively,filterOnVerticesapplies a filter on the vertices of the graph. Edges whose source and/or target do not satisfy the vertex predicate are removed from the resulting edge dataset. Thesubgraphmethod can be used to apply a filter function to the vertices and the edges at the same time.
Graph<Long, Long, Long> graph = ...
graph.subgraph(
new FilterFunction<Vertex<Long, Long>>() {
public boolean filter(Vertex<Long, Long> vertex) {
// keep only vertices with positive values
return (vertex.getValue() > 0);
}
},
new FilterFunction<Edge<Long, Long>>() {
public boolean filter(Edge<Long, Long> edge) {
// keep only edges with negative values
return (edge.getValue() < 0);
}
})val graph: Graph[Long, Long, Long] = ...
// keep only vertices with positive values
// and only edges with negative values
graph.subgraph((vertex => vertex.getValue > 0), (edge => edge.getValue < 0))
- Join: Gelly provides specialized methods for joining the vertex and edge datasets with other input datasets.
joinWithVerticesjoins the vertices with aTuple2input data set. The join is performed using the vertex ID and the first field of theTuple2input as the join keys. The method returns a newGraphwhere the vertex values have been updated according to a provided user-defined transformation function. Similarly, an input dataset can be joined with the edges, using one of three methods.joinWithEdgesexpects an inputDataSetofTuple3and joins on the composite key of both source and target vertex IDs.joinWithEdgesOnSourceexpects aDataSetofTuple2and joins on the source key of the edges and the first attribute of the input dataset andjoinWithEdgesOnTargetexpects aDataSetofTuple2and joins on the target key of the edges and the first attribute of the input dataset. All three methods apply a transformation function on the edge and the input data set values. Note that if the input dataset contains a key multiple times, all Gelly join methods will only consider the first value encountered.
Graph<Long, Double, Double> network = ...
DataSet<Tuple2<Long, Long>> vertexOutDegrees = network.outDegrees();
// assign the transition probabilities as the edge weights
Graph<Long, Double, Double> networkWithWeights = network.joinWithEdgesOnSource(vertexOutDegrees,
new VertexJoinFunction<Double, Long>() {
public Double vertexJoin(Double vertexValue, Long inputValue) {
return vertexValue / inputValue;
}
});val network: Graph[Long, Double, Double] = ...
val vertexOutDegrees: DataSet[(Long, Long)] = network.outDegrees
// assign the transition probabilities as the edge weights
val networkWithWeights = network.joinWithEdgesOnSource(vertexOutDegrees, (v1: Double, v2: Long) => v1 / v2)-
Reverse: the
reverse()method returns a newGraphwhere the direction of all edges has been reversed. -
Undirected: In Gelly, a
Graphis always directed. Undirected graphs can be represented by adding all opposite-direction edges to a graph. For this purpose, Gelly provides thegetUndirected()method. -
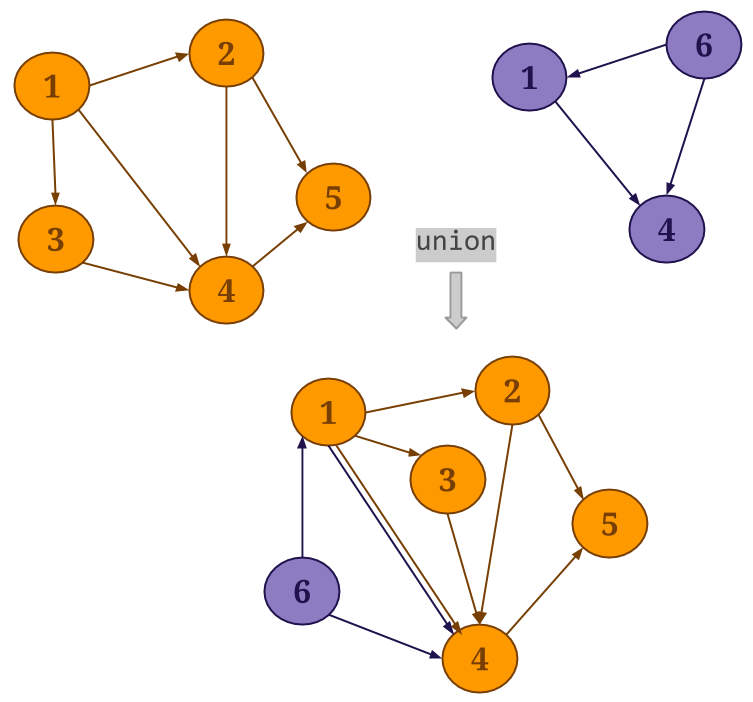
Union: Gelly’s
union()method performs a union operation on the vertex and edge sets of the specified graph and the current graph. Duplicate vertices are removed from the resultingGraph, while if duplicate edges exist, these will be preserved.
-
Difference: Gelly’s
difference()method performs a difference on the vertex and edge sets of the current graph and the specified graph. -
Intersect: Gelly’s
intersect()method performs an intersect on the edge sets of the current graph and the specified graph. The result is a newGraphthat contains all edges that exist in both input graphs. Two edges are considered equal, if they have the same source identifier, target identifier and edge value. Vertices in the resulting graph have no value. If vertex values are required, one can for example retrieve them from one of the input graphs using thejoinWithVertices()method. Depending on the parameterdistinct, equal edges are either contained once in the resultingGraphor as often as there are pairs of equal edges in the input graphs.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create first graph from edges {(1, 3, 12) (1, 3, 13), (1, 3, 13)}
List<Edge<Long, Long>> edges1 = ...
Graph<Long, NullValue, Long> graph1 = Graph.fromCollection(edges1, env);
// create second graph from edges {(1, 3, 13)}
List<Edge<Long, Long>> edges2 = ...
Graph<Long, NullValue, Long> graph2 = Graph.fromCollection(edges2, env);
// Using distinct = true results in {(1,3,13)}
Graph<Long, NullValue, Long> intersect1 = graph1.intersect(graph2, true);
// Using distinct = false results in {(1,3,13),(1,3,13)} as there is one edge pair
Graph<Long, NullValue, Long> intersect2 = graph1.intersect(graph2, false);val env = ExecutionEnvironment.getExecutionEnvironment
// create first graph from edges {(1, 3, 12) (1, 3, 13), (1, 3, 13)}
val edges1: List[Edge[Long, Long]] = ...
val graph1 = Graph.fromCollection(edges1, env)
// create second graph from edges {(1, 3, 13)}
val edges2: List[Edge[Long, Long]] = ...
val graph2 = Graph.fromCollection(edges2, env)
// Using distinct = true results in {(1,3,13)}
val intersect1 = graph1.intersect(graph2, true)
// Using distinct = false results in {(1,3,13),(1,3,13)} as there is one edge pair
val intersect2 = graph1.intersect(graph2, false)Graph Mutations
Gelly includes the following methods for adding and removing vertices and edges from an input Graph:
// adds a Vertex to the Graph. If the Vertex already exists, it will not be added again.
Graph<K, VV, EV> addVertex(final Vertex<K, VV> vertex)
// adds a list of vertices to the Graph. If the vertices already exist in the graph, they will not be added once more.
Graph<K, VV, EV> addVertices(List<Vertex<K, VV>> verticesToAdd)
// adds an Edge to the Graph. If the source and target vertices do not exist in the graph, they will also be added.
Graph<K, VV, EV> addEdge(Vertex<K, VV> source, Vertex<K, VV> target, EV edgeValue)
// adds a list of edges to the Graph. When adding an edge for a non-existing set of vertices, the edge is considered invalid and ignored.
Graph<K, VV, EV> addEdges(List<Edge<K, EV>> newEdges)
// removes the given Vertex and its edges from the Graph.
Graph<K, VV, EV> removeVertex(Vertex<K, VV> vertex)
// removes the given list of vertices and their edges from the Graph
Graph<K, VV, EV> removeVertices(List<Vertex<K, VV>> verticesToBeRemoved)
// removes *all* edges that match the given Edge from the Graph.
Graph<K, VV, EV> removeEdge(Edge<K, EV> edge)
// removes *all* edges that match the edges in the given list
Graph<K, VV, EV> removeEdges(List<Edge<K, EV>> edgesToBeRemoved)// adds a Vertex to the Graph. If the Vertex already exists, it will not be added again.
addVertex(vertex: Vertex[K, VV])
// adds a list of vertices to the Graph. If the vertices already exist in the graph, they will not be added once more.
addVertices(verticesToAdd: List[Vertex[K, VV]])
// adds an Edge to the Graph. If the source and target vertices do not exist in the graph, they will also be added.
addEdge(source: Vertex[K, VV], target: Vertex[K, VV], edgeValue: EV)
// adds a list of edges to the Graph. When adding an edge for a non-existing set of vertices, the edge is considered invalid and ignored.
addEdges(edges: List[Edge[K, EV]])
// removes the given Vertex and its edges from the Graph.
removeVertex(vertex: Vertex[K, VV])
// removes the given list of vertices and their edges from the Graph
removeVertices(verticesToBeRemoved: List[Vertex[K, VV]])
// removes *all* edges that match the given Edge from the Graph.
removeEdge(edge: Edge[K, EV])
// removes *all* edges that match the edges in the given list
removeEdges(edgesToBeRemoved: List[Edge[K, EV]])Neighborhood Methods
Neighborhood methods allow vertices to perform an aggregation on their first-hop neighborhood.
reduceOnEdges() can be used to compute an aggregation on the values of the neighboring edges of a vertex and reduceOnNeighbors() can be used to compute an aggregation on the values of the neighboring vertices. These methods assume associative and commutative aggregations and exploit combiners internally, significantly improving performance.
The neighborhood scope is defined by the EdgeDirection parameter, which takes the values IN, OUT or ALL. IN will gather all in-coming edges (neighbors) of a vertex, OUT will gather all out-going edges (neighbors), while ALL will gather all edges (neighbors).
For example, assume that you want to select the minimum weight of all out-edges for each vertex in the following graph:
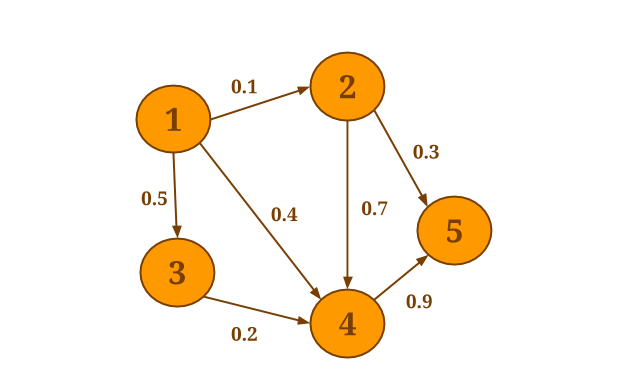
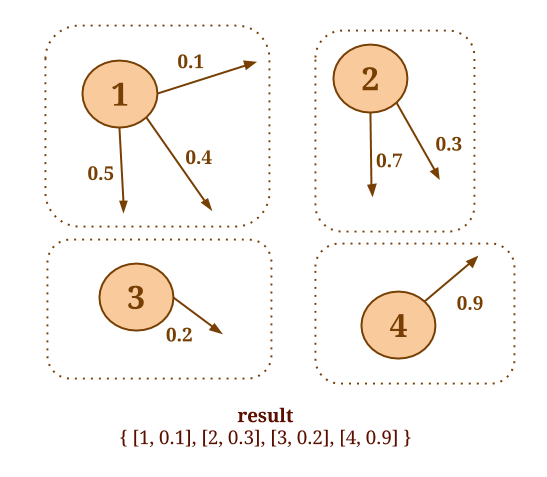
The following code will collect the out-edges for each vertex and apply the SelectMinWeight() user-defined function on each of the resulting neighborhoods:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Long, Double>> minWeights = graph.reduceOnEdges(new SelectMinWeight(), EdgeDirection.OUT);
// user-defined function to select the minimum weight
static final class SelectMinWeight implements ReduceEdgesFunction<Double> {
@Override
public Double reduceEdges(Double firstEdgeValue, Double secondEdgeValue) {
return Math.min(firstEdgeValue, secondEdgeValue);
}
}val graph: Graph[Long, Long, Double] = ...
val minWeights = graph.reduceOnEdges(new SelectMinWeight, EdgeDirection.OUT)
// user-defined function to select the minimum weight
final class SelectMinWeight extends ReduceEdgesFunction[Double] {
override def reduceEdges(firstEdgeValue: Double, secondEdgeValue: Double): Double = {
Math.min(firstEdgeValue, secondEdgeValue)
}
}
Similarly, assume that you would like to compute the sum of the values of all in-coming neighbors, for every vertex. The following code will collect the in-coming neighbors for each vertex and apply the SumValues() user-defined function on each neighborhood:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Long, Long>> verticesWithSum = graph.reduceOnNeighbors(new SumValues(), EdgeDirection.IN);
// user-defined function to sum the neighbor values
static final class SumValues implements ReduceNeighborsFunction<Long> {
@Override
public Long reduceNeighbors(Long firstNeighbor, Long secondNeighbor) {
return firstNeighbor + secondNeighbor;
}
}val graph: Graph[Long, Long, Double] = ...
val verticesWithSum = graph.reduceOnNeighbors(new SumValues, EdgeDirection.IN)
// user-defined function to sum the neighbor values
final class SumValues extends ReduceNeighborsFunction[Long] {
override def reduceNeighbors(firstNeighbor: Long, secondNeighbor: Long): Long = {
firstNeighbor + secondNeighbor
}
}
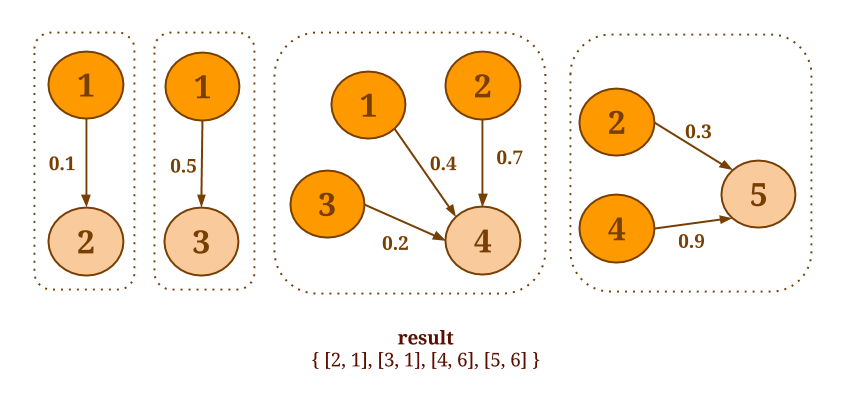
When the aggregation function is not associative and commutative or when it is desirable to return more than one values per vertex, one can use the more general
groupReduceOnEdges() and groupReduceOnNeighbors() methods.
These methods return zero, one or more values per vertex and provide access to the whole neighborhood.
For example, the following code will output all the vertex pairs which are connected with an edge having a weight of 0.5 or more:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> vertexPairs = graph.groupReduceOnNeighbors(new SelectLargeWeightNeighbors(), EdgeDirection.OUT);
// user-defined function to select the neighbors which have edges with weight > 0.5
static final class SelectLargeWeightNeighbors implements NeighborsFunctionWithVertexValue<Long, Long, Double,
Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> {
@Override
public void iterateNeighbors(Vertex<Long, Long> vertex,
Iterable<Tuple2<Edge<Long, Double>, Vertex<Long, Long>>> neighbors,
Collector<Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> out) {
for (Tuple2<Edge<Long, Double>, Vertex<Long, Long>> neighbor : neighbors) {
if (neighbor.f0.f2 > 0.5) {
out.collect(new Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>(vertex, neighbor.f1));
}
}
}
}val graph: Graph[Long, Long, Double] = ...
val vertexPairs = graph.groupReduceOnNeighbors(new SelectLargeWeightNeighbors, EdgeDirection.OUT)
// user-defined function to select the neighbors which have edges with weight > 0.5
final class SelectLargeWeightNeighbors extends NeighborsFunctionWithVertexValue[Long, Long, Double,
(Vertex[Long, Long], Vertex[Long, Long])] {
override def iterateNeighbors(vertex: Vertex[Long, Long],
neighbors: Iterable[(Edge[Long, Double], Vertex[Long, Long])],
out: Collector[(Vertex[Long, Long], Vertex[Long, Long])]) = {
for (neighbor <- neighbors) {
if (neighbor._1.getValue() > 0.5) {
out.collect(vertex, neighbor._2);
}
}
}
}When the aggregation computation does not require access to the vertex value (for which the aggregation is performed), it is advised to use the more efficient EdgesFunction and NeighborsFunction for the user-defined functions. When access to the vertex value is required, one should use EdgesFunctionWithVertexValue and NeighborsFunctionWithVertexValue instead.
Iterative Graph Processing
Gelly exploits Flink’s efficient iteration operators to support large-scale iterative graph processing. Currently, we provide implementations of the popular scatter-gather iterative model and a variation of Gather-Sum-Apply. In the following sections, we describe these models and show how you can use them in Gelly.
Scatter-Gather Iterations
The scatter-gather model, also known as “signal/collect” model, expresses computation from the perspective of a vertex in the graph. The computation proceeds in synchronized iteration steps, called supersteps. In each superstep, a vertex produces messages for other vertices and updates its value based on the messages it receives. To use scatter-gather iterations in Gelly, the user only needs to define how a vertex behaves in each superstep:
- Messaging: corresponds to the scatter phase and produces the messages that a vertex will send to other vertices.
- Value Update: corresponds to the gather phase and updates the vertex value using the received messages.
Gelly provides methods for scatter-gather iterations. The user only needs to implement two functions, corresponding to the scatter and gather phases. The first function is a MessagingFunction, which allows a vertex to send out messages for other vertices. Messages are recieved during the same superstep as they are sent. The second function is VertexUpdateFunction, which defines how a vertex will update its value based on the received messages.
These functions and the maximum number of iterations to run are given as parameters to Gelly’s runScatterGatherIteration. This method will execute the scatter-gather iteration on the input Graph and return a new Graph, with updated vertex values.
A scatter-gather iteration can be extended with information such as the total number of vertices, the in degree and out degree. Additionally, the neighborhood type (in/out/all) over which to run the scatter-gather iteration can be specified. By default, the updates from the in-neighbors are used to modify the current vertex’s state and messages are sent to out-neighbors.
Let us consider computing Single-Source-Shortest-Paths with scatter-gather iterations on the following graph and let vertex 1 be the source. In each superstep, each vertex sends a candidate distance message to all its neighbors. The message value is the sum of the current value of the vertex and the edge weight connecting this vertex with its neighbor. Upon receiving candidate distance messages, each vertex calculates the minimum distance and, if a shorter path has been discovered, it updates its value. If a vertex does not change its value during a superstep, then it does not produce messages for its neighbors for the next superstep. The algorithm converges when there are no value updates.
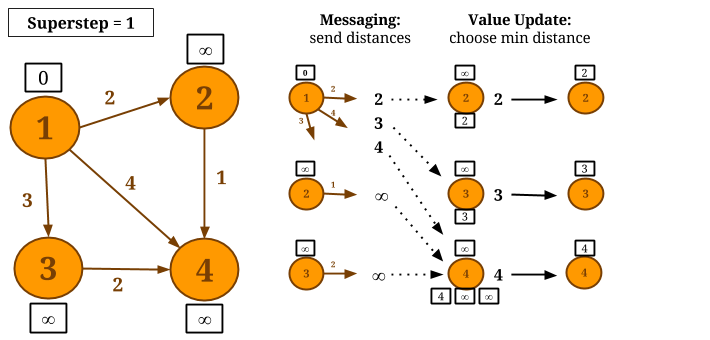
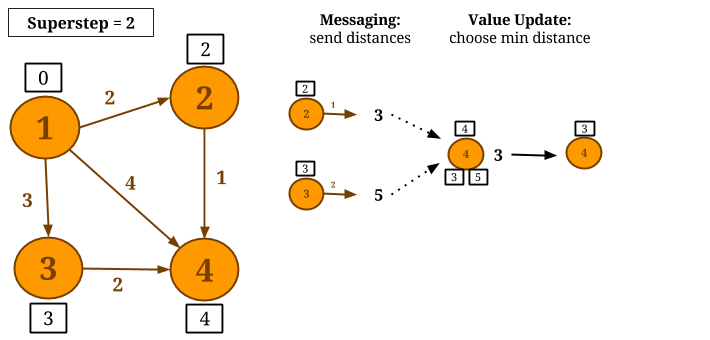
// read the input graph
Graph<Long, Double, Double> graph = ...
// define the maximum number of iterations
int maxIterations = 10;
// Execute the scatter-gather iteration
Graph<Long, Double, Double> result = graph.runScatterGatherIteration(
new VertexDistanceUpdater(), new MinDistanceMessenger(), maxIterations);
// Extract the vertices as the result
DataSet<Vertex<Long, Double>> singleSourceShortestPaths = result.getVertices();
// - - - UDFs - - - //
// scatter: messaging
public static final class MinDistanceMessenger extends MessagingFunction<Long, Double, Double, Double> {
public void sendMessages(Vertex<Long, Double> vertex) {
for (Edge<Long, Double> edge : getEdges()) {
sendMessageTo(edge.getTarget(), vertex.getValue() + edge.getValue());
}
}
}
// gather: vertex update
public static final class VertexDistanceUpdater extends VertexUpdateFunction<Long, Double, Double> {
public void updateVertex(Vertex<Long, Double> vertex, MessageIterator<Double> inMessages) {
Double minDistance = Double.MAX_VALUE;
for (double msg : inMessages) {
if (msg < minDistance) {
minDistance = msg;
}
}
if (vertex.getValue() > minDistance) {
setNewVertexValue(minDistance);
}
}
}// read the input graph
val graph: Graph[Long, Double, Double] = ...
// define the maximum number of iterations
val maxIterations = 10
// Execute the scatter-gather iteration
val result = graph.runScatterGatherIteration(new VertexDistanceUpdater, new MinDistanceMessenger, maxIterations)
// Extract the vertices as the result
val singleSourceShortestPaths = result.getVertices
// - - - UDFs - - - //
// messaging
final class MinDistanceMessenger extends MessagingFunction[Long, Double, Double, Double] {
override def sendMessages(vertex: Vertex[Long, Double]) = {
for (edge: Edge[Long, Double] <- getEdges) {
sendMessageTo(edge.getTarget, vertex.getValue + edge.getValue)
}
}
}
// vertex update
final class VertexDistanceUpdater extends VertexUpdateFunction[Long, Double, Double] {
override def updateVertex(vertex: Vertex[Long, Double], inMessages: MessageIterator[Double]) = {
var minDistance = Double.MaxValue
while (inMessages.hasNext) {
val msg = inMessages.next
if (msg < minDistance) {
minDistance = msg
}
}
if (vertex.getValue > minDistance) {
setNewVertexValue(minDistance)
}
}
}Configuring a Scatter-Gather Iteration
A scatter-gather iteration can be configured using a ScatterGatherConfiguration object.
Currently, the following parameters can be specified:
-
Name: The name for the scatter-gather iteration. The name is displayed in logs and messages and can be specified using the
setName()method. -
Parallelism: The parallelism for the iteration. It can be set using the
setParallelism()method. -
Solution set in unmanaged memory: Defines whether the solution set is kept in managed memory (Flink’s internal way of keeping objects in serialized form) or as a simple object map. By default, the solution set runs in managed memory. This property can be set using the
setSolutionSetUnmanagedMemory()method. -
Aggregators: Iteration aggregators can be registered using the
registerAggregator()method. An iteration aggregator combines all aggregates globally once per superstep and makes them available in the next superstep. Registered aggregators can be accessed inside the user-definedVertexUpdateFunctionandMessagingFunction. -
Broadcast Variables: DataSets can be added as Broadcast Variables to the
VertexUpdateFunctionandMessagingFunction, using theaddBroadcastSetForUpdateFunction()andaddBroadcastSetForMessagingFunction()methods, respectively. -
Number of Vertices: Accessing the total number of vertices within the iteration. This property can be set using the
setOptNumVertices()method. The number of vertices can then be accessed in the vertex update function and in the messaging function using thegetNumberOfVertices()method. If the option is not set in the configuration, this method will return -1. -
Degrees: Accessing the in/out degree for a vertex within an iteration. This property can be set using the
setOptDegrees()method. The in/out degrees can then be accessed in the vertex update function and in the messaging function, per vertex using thegetInDegree()andgetOutDegree()methods. If the degrees option is not set in the configuration, these methods will return -1. -
Messaging Direction: By default, a vertex sends messages to its out-neighbors and updates its value based on messages received from its in-neighbors. This configuration option allows users to change the messaging direction to either
EdgeDirection.IN,EdgeDirection.OUT,EdgeDirection.ALL. The messaging direction also dictates the update direction which would beEdgeDirection.OUT,EdgeDirection.INandEdgeDirection.ALL, respectively. This property can be set using thesetDirection()method.
Graph<Long, Double, Double> graph = ...
// configure the iteration
ScatterGatherConfiguration parameters = new ScatterGatherConfiguration();
// set the iteration name
parameters.setName("Gelly Iteration");
// set the parallelism
parameters.setParallelism(16);
// register an aggregator
parameters.registerAggregator("sumAggregator", new LongSumAggregator());
// run the scatter-gather iteration, also passing the configuration parameters
Graph<Long, Double, Double> result =
graph.runScatterGatherIteration(
new VertexUpdater(), new Messenger(), maxIterations, parameters);
// user-defined functions
public static final class VertexUpdater extends VertexUpdateFunction {
LongSumAggregator aggregator = new LongSumAggregator();
public void preSuperstep() {
// retrieve the Aggregator
aggregator = getIterationAggregator("sumAggregator");
}
public void updateVertex(Vertex<Long, Long> vertex, MessageIterator inMessages) {
//do some computation
Long partialValue = ...
// aggregate the partial value
aggregator.aggregate(partialValue);
// update the vertex value
setNewVertexValue(...);
}
}
public static final class Messenger extends MessagingFunction {...}val graph: Graph[Long, Double, Double] = ...
val parameters = new ScatterGatherConfiguration
// set the iteration name
parameters.setName("Gelly Iteration")
// set the parallelism
parameters.setParallelism(16)
// register an aggregator
parameters.registerAggregator("sumAggregator", new LongSumAggregator)
// run the scatter-gather iteration, also passing the configuration parameters
val result = graph.runScatterGatherIteration(new VertexUpdater, new Messenger, maxIterations, parameters)
// user-defined functions
final class VertexUpdater extends VertexUpdateFunction {
var aggregator = new LongSumAggregator
override def preSuperstep {
// retrieve the Aggregator
aggregator = getIterationAggregator("sumAggregator")
}
override def updateVertex(vertex: Vertex[Long, Long], inMessages: MessageIterator[Long]) {
//do some computation
val partialValue = ...
// aggregate the partial value
aggregator.aggregate(partialValue)
// update the vertex value
setNewVertexValue(...)
}
}
final class Messenger extends MessagingFunction {...}The following example illustrates the usage of the degree as well as the number of vertices options.
Graph<Long, Double, Double> graph = ...
// configure the iteration
ScatterGatherConfiguration parameters = new ScatterGatherConfiguration();
// set the number of vertices option to true
parameters.setOptNumVertices(true);
// set the degree option to true
parameters.setOptDegrees(true);
// run the scatter-gather iteration, also passing the configuration parameters
Graph<Long, Double, Double> result =
graph.runScatterGatherIteration(
new VertexUpdater(), new Messenger(), maxIterations, parameters);
// user-defined functions
public static final class VertexUpdater {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}
public static final class Messenger {
...
// retrieve the vertex out-degree
outDegree = getOutDegree();
...
}val graph: Graph[Long, Double, Double] = ...
// configure the iteration
val parameters = new ScatterGatherConfiguration
// set the number of vertices option to true
parameters.setOptNumVertices(true)
// set the degree option to true
parameters.setOptDegrees(true)
// run the scatter-gather iteration, also passing the configuration parameters
val result = graph.runScatterGatherIteration(new VertexUpdater, new Messenger, maxIterations, parameters)
// user-defined functions
final class VertexUpdater {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}
final class Messenger {
...
// retrieve the vertex out-degree
val outDegree = getOutDegree
...
}The following example illustrates the usage of the edge direction option. Vertices update their values to contain a list of all their in-neighbors.
Graph<Long, HashSet<Long>, Double> graph = ...
// configure the iteration
ScatterGatherConfiguration parameters = new ScatterGatherConfiguration();
// set the messaging direction
parameters.setDirection(EdgeDirection.IN);
// run the scatter-gather iteration, also passing the configuration parameters
DataSet<Vertex<Long, HashSet<Long>>> result =
graph.runScatterGatherIteration(
new VertexUpdater(), new Messenger(), maxIterations, parameters)
.getVertices();
// user-defined functions
public static final class VertexUpdater {...}
public static final class Messenger {...}val graph: Graph[Long, HashSet[Long], Double] = ...
// configure the iteration
val parameters = new ScatterGatherConfiguration
// set the messaging direction
parameters.setDirection(EdgeDirection.IN)
// run the scatter-gather iteration, also passing the configuration parameters
val result = graph.runScatterGatherIteration(new VertexUpdater, new Messenger, maxIterations, parameters)
.getVertices
// user-defined functions
final class VertexUpdater {...}
final class Messenger {...}Gather-Sum-Apply Iterations
Like in the scatter-gather model, Gather-Sum-Apply also proceeds in synchronized iterative steps, called supersteps. Each superstep consists of the following three phases:
- Gather: a user-defined function is invoked in parallel on the edges and neighbors of each vertex, producing a partial value.
- Sum: the partial values produced in the Gather phase are aggregated to a single value, using a user-defined reducer.
- Apply: each vertex value is updated by applying a function on the current value and the aggregated value produced by the Sum phase.
Let us consider computing Single-Source-Shortest-Paths with GSA on the following graph and let vertex 1 be the source. During the Gather phase, we calculate the new candidate distances, by adding each vertex value with the edge weight. In Sum, the candidate distances are grouped by vertex ID and the minimum distance is chosen. In Apply, the newly calculated distance is compared to the current vertex value and the minimum of the two is assigned as the new value of the vertex.
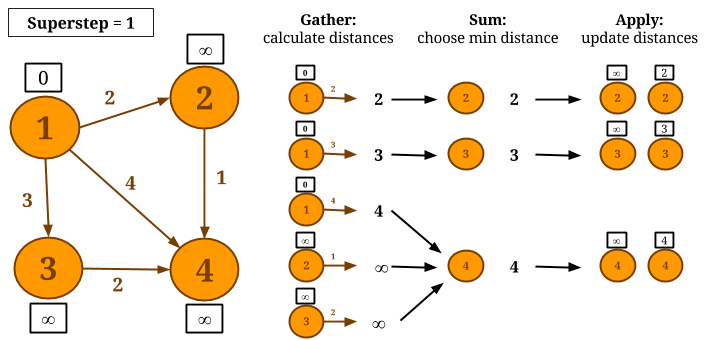
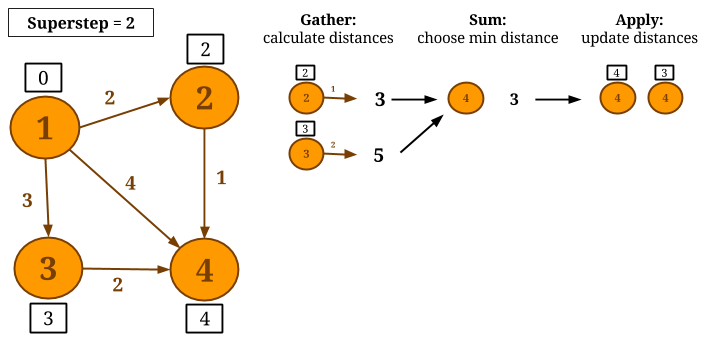
Notice that, if a vertex does not change its value during a superstep, it will not calculate candidate distance during the next superstep. The algorithm converges when no vertex changes value. The resulting graph after the algorithm converges is shown below.

To implement this example in Gelly GSA, the user only needs to call the runGatherSumApplyIteration method on the input graph and provide the GatherFunction, SumFunction and ApplyFunction UDFs. Iteration synchronization, grouping, value updates and convergence are handled by the system:
// read the input graph
Graph<Long, Double, Double> graph = ...
// define the maximum number of iterations
int maxIterations = 10;
// Execute the GSA iteration
Graph<Long, Double, Double> result = graph.runGatherSumApplyIteration(
new CalculateDistances(), new ChooseMinDistance(), new UpdateDistance(), maxIterations);
// Extract the vertices as the result
DataSet<Vertex<Long, Double>> singleSourceShortestPaths = result.getVertices();
// - - - UDFs - - - //
// Gather
private static final class CalculateDistances extends GatherFunction<Double, Double, Double> {
public Double gather(Neighbor<Double, Double> neighbor) {
return neighbor.getNeighborValue() + neighbor.getEdgeValue();
}
}
// Sum
private static final class ChooseMinDistance extends SumFunction<Double, Double, Double> {
public Double sum(Double newValue, Double currentValue) {
return Math.min(newValue, currentValue);
}
}
// Apply
private static final class UpdateDistance extends ApplyFunction<Long, Double, Double> {
public void apply(Double newDistance, Double oldDistance) {
if (newDistance < oldDistance) {
setResult(newDistance);
}
}
}// read the input graph
val graph: Graph[Long, Double, Double] = ...
// define the maximum number of iterations
val maxIterations = 10
// Execute the GSA iteration
val result = graph.runGatherSumApplyIteration(new CalculateDistances, new ChooseMinDistance, new UpdateDistance, maxIterations)
// Extract the vertices as the result
val singleSourceShortestPaths = result.getVertices
// - - - UDFs - - - //
// Gather
final class CalculateDistances extends GatherFunction[Double, Double, Double] {
override def gather(neighbor: Neighbor[Double, Double]): Double = {
neighbor.getNeighborValue + neighbor.getEdgeValue
}
}
// Sum
final class ChooseMinDistance extends SumFunction[Double, Double, Double] {
override def sum(newValue: Double, currentValue: Double): Double = {
Math.min(newValue, currentValue)
}
}
// Apply
final class UpdateDistance extends ApplyFunction[Long, Double, Double] {
override def apply(newDistance: Double, oldDistance: Double) = {
if (newDistance < oldDistance) {
setResult(newDistance)
}
}
}Note that gather takes a Neighbor type as an argument. This is a convenience type which simply wraps a vertex with its neighboring edge.
For more examples of how to implement algorithms with the Gather-Sum-Apply model, check the GSAPageRank and GSAConnectedComponents library methods of Gelly.
Configuring a Gather-Sum-Apply Iteration
A GSA iteration can be configured using a GSAConfiguration object.
Currently, the following parameters can be specified:
-
Name: The name for the GSA iteration. The name is displayed in logs and messages and can be specified using the
setName()method. -
Parallelism: The parallelism for the iteration. It can be set using the
setParallelism()method. -
Solution set in unmanaged memory: Defines whether the solution set is kept in managed memory (Flink’s internal way of keeping objects in serialized form) or as a simple object map. By default, the solution set runs in managed memory. This property can be set using the
setSolutionSetUnmanagedMemory()method. -
Aggregators: Iteration aggregators can be registered using the
registerAggregator()method. An iteration aggregator combines all aggregates globally once per superstep and makes them available in the next superstep. Registered aggregators can be accessed inside the user-definedGatherFunction,SumFunctionandApplyFunction. -
Broadcast Variables: DataSets can be added as Broadcast Variables to the
GatherFunction,SumFunctionandApplyFunction, using the methodsaddBroadcastSetForGatherFunction(),addBroadcastSetForSumFunction()andaddBroadcastSetForApplyFunctionmethods, respectively. -
Number of Vertices: Accessing the total number of vertices within the iteration. This property can be set using the
setOptNumVertices()method. The number of vertices can then be accessed in the gather, sum and/or apply functions by using thegetNumberOfVertices()method. If the option is not set in the configuration, this method will return -1. -
Neighbor Direction: By default values are gathered from the out neighbors of the Vertex. This can be modified using the
setDirection()method.
The following example illustrates the usage of the number of vertices option.
Graph<Long, Double, Double> graph = ...
// configure the iteration
GSAConfiguration parameters = new GSAConfiguration();
// set the number of vertices option to true
parameters.setOptNumVertices(true);
// run the gather-sum-apply iteration, also passing the configuration parameters
Graph<Long, Long, Long> result = graph.runGatherSumApplyIteration(
new Gather(), new Sum(), new Apply(),
maxIterations, parameters);
// user-defined functions
public static final class Gather {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}
public static final class Sum {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}
public static final class Apply {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}val graph: Graph[Long, Double, Double] = ...
// configure the iteration
val parameters = new GSAConfiguration
// set the number of vertices option to true
parameters.setOptNumVertices(true)
// run the gather-sum-apply iteration, also passing the configuration parameters
val result = graph.runGatherSumApplyIteration(new Gather, new Sum, new Apply, maxIterations, parameters)
// user-defined functions
final class Gather {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}
final class Sum {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}
final class Apply {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}The following example illustrates the usage of the edge direction option.
Graph<Long, HashSet<Long>, Double> graph = ...
// configure the iteration
GSAConfiguration parameters = new GSAConfiguration();
// set the messaging direction
parameters.setDirection(EdgeDirection.IN);
// run the gather-sum-apply iteration, also passing the configuration parameters
DataSet<Vertex<Long, HashSet<Long>>> result =
graph.runGatherSumApplyIteration(
new Gather(), new Sum(), new Apply(), maxIterations, parameters)
.getVertices();val graph: Graph[Long, HashSet[Long], Double] = ...
// configure the iteration
val parameters = new GSAConfiguration
// set the messaging direction
parameters.setDirection(EdgeDirection.IN)
// run the gather-sum-apply iteration, also passing the configuration parameters
val result = graph.runGatherSumApplyIteration(new Gather, new Sum, new Apply, maxIterations, parameters)
.getVertices()Scatter-Gather and GSA Comparison
As seen in the examples above, Gather-Sum-Apply iterations are quite similar to scatter-gather iterations. In fact, any algorithm which can be expressed as a GSA iteration can also be written in the scatter-gather model. The messaging phase of the scatter-gather model is equivalent to the Gather and Sum steps of GSA: Gather can be seen as the phase where the messages are produced and Sum as the phase where they are routed to the target vertex. Similarly, the value update phase corresponds to the Apply step.
The main difference between the two implementations is that the Gather phase of GSA parallelizes the computation over the edges, while the messaging phase distributes the computation over the vertices. Using the SSSP examples above, we see that in the first superstep of the scatter-gather case, vertices 1, 2 and 3 produce messages in parallel. Vertex 1 produces 3 messages, while vertices 2 and 3 produce one message each. In the GSA case on the other hand, the computation is parallelized over the edges: the three candidate distance values of vertex 1 are produced in parallel. Thus, if the Gather step contains “heavy” computation, it might be a better idea to use GSA and spread out the computation, instead of burdening a single vertex. Another case when parallelizing over the edges might prove to be more efficient is when the input graph is skewed (some vertices have a lot more neighbors than others).
Another difference between the two implementations is that the scatter-gather implementation uses a coGroup operator internally, while GSA uses a reduce. Therefore, if the function that combines neighbor values (messages) requires the whole group of values for the computation, scatter-gather should be used. If the update function is associative and commutative, then the GSA’s reducer is expected to give a more efficient implementation, as it can make use of a combiner.
Another thing to note is that GSA works strictly on neighborhoods, while in the scatter-gather model, a vertex can send a message to any vertex, given that it knows its vertex ID, regardless of whether it is a neighbor. Finally, in Gelly’s scatter-gather implementation, one can choose the messaging direction, i.e. the direction in which updates propagate. GSA does not support this yet, so each vertex will be updated based on the values of its in-neighbors only.
Graph Validation
Gelly provides a simple utility for performing validation checks on input graphs. Depending on the application context, a graph may or may not be valid according to certain criteria. For example, a user might need to validate whether their graph contains duplicate edges or whether its structure is bipartite. In order to validate a graph, one can define a custom GraphValidator and implement its validate() method. InvalidVertexIdsValidator is Gelly’s pre-defined validator. It checks that the edge set contains valid vertex IDs, i.e. that all edge IDs
also exist in the vertex IDs set.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create a list of vertices with IDs = {1, 2, 3, 4, 5}
List<Vertex<Long, Long>> vertices = ...
// create a list of edges with IDs = {(1, 2) (1, 3), (2, 4), (5, 6)}
List<Edge<Long, Long>> edges = ...
Graph<Long, Long, Long> graph = Graph.fromCollection(vertices, edges, env);
// will return false: 6 is an invalid ID
graph.validate(new InvalidVertexIdsValidator<Long, Long, Long>());val env = ExecutionEnvironment.getExecutionEnvironment
// create a list of vertices with IDs = {1, 2, 3, 4, 5}
val vertices: List[Vertex[Long, Long]] = ...
// create a list of edges with IDs = {(1, 2) (1, 3), (2, 4), (5, 6)}
val edges: List[Edge[Long, Long]] = ...
val graph = Graph.fromCollection(vertices, edges, env)
// will return false: 6 is an invalid ID
graph.validate(new InvalidVertexIdsValidator[Long, Long, Long])Library Methods
Gelly has a growing collection of graph algorithms for easily analyzing large-scale Graphs. So far, the following library methods are implemented:
- Community Detection
- Label Propagation
- Connected Components
- GSA Connected Components
- PageRank
- GSA PageRank
- Single Source Shortest Paths
- GSA Single Source Shortest Paths
- GSA Triangle Count
- Triangle Enumerator
- Summarization
Gelly’s library methods can be used by simply calling the run() method on the input graph:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, NullValue> graph = ...
// run Label Propagation for 30 iterations to detect communities on the input graph
DataSet<Vertex<Long, Long>> verticesWithCommunity = graph.run(new LabelPropagation<Long>(30));
// print the result
verticesWithCommunity.print();val env = ExecutionEnvironment.getExecutionEnvironment
val graph: Graph[Long, Long, NullValue] = ...
// run Label Propagation for 30 iterations to detect communities on the input graph
val verticesWithCommunity = graph.run(new LabelPropagation[Long](30))
// print the result
verticesWithCommunity.printCommunity Detection
Overview
In graph theory, communities refer to groups of nodes that are well connected internally, but sparsely connected to other groups. This library method is an implementation of the community detection algorithm described in the paper Towards real-time community detection in large networks.
Details
The algorithm is implemented using scatter-gather iterations.
Initially, each vertex is assigned a Tuple2 containing its initial value along with a score equal to 1.0.
In each iteration, vertices send their labels and scores to their neighbors. Upon receiving messages from its neighbors,
a vertex chooses the label with the highest score and subsequently re-scores it using the edge values,
a user-defined hop attenuation parameter, delta, and the superstep number.
The algorithm converges when vertices no longer update their value or when the maximum number of iterations
is reached.
Usage
The algorithm takes as input a Graph with any vertex type, Long vertex values, and Double edge values. It returns a Graph of the same type as the input,
where the vertex values correspond to the community labels, i.e. two vertices belong to the same community if they have the same vertex value.
The constructor takes two parameters:
maxIterations: the maximum number of iterations to run.delta: the hop attenuation parameter, with default value 0.5.
Label Propagation
Overview
This is an implementation of the well-known Label Propagation algorithm described in this paper. The algorithm discovers communities in a graph, by iteratively propagating labels between neighbors. Unlike the Community Detection library method, this implementation does not use scores associated with the labels.
Details
The algorithm is implemented using scatter-gather iterations.
Labels are expected to be of type Comparable and are initialized using the vertex values of the input Graph.
The algorithm iteratively refines discovered communities by propagating labels. In each iteration, a vertex adopts
the label that is most frequent among its neighbors’ labels. In case of a tie (i.e. two or more labels appear with the
same frequency), the algorithm picks the greater label. The algorithm converges when no vertex changes its value or
the maximum number of iterations has been reached. Note that different initializations might lead to different results.
Usage
The algorithm takes as input a Graph with a Comparable vertex type, a Comparable vertex value type and an arbitrary edge value type.
It returns a DataSet of vertices, where the vertex value corresponds to the community in which this vertex belongs after convergence.
The constructor takes one parameter:
maxIterations: the maximum number of iterations to run.
Connected Components
Overview
This is an implementation of the Weakly Connected Components algorithm. Upon convergence, two vertices belong to the same component, if there is a path from one to the other, without taking edge direction into account.
Details
The algorithm is implemented using scatter-gather iterations. This implementation assumes that the vertex values of the input Graph are initialized with Long component IDs. The vertices propagate their current component ID in iterations. Upon receiving component IDs from its neighbors, a vertex adopts a new component ID if its value is lower than its current component ID. The algorithm converges when vertices no longer update their component ID value or when the maximum number of iterations has been reached.
Usage
The result is a DataSet of vertices, where the vertex value corresponds to the assigned component.
The constructor takes one parameter:
maxIterations: the maximum number of iterations to run.
GSA Connected Components
The algorithm is implemented using gather-sum-apply iterations.
See the Connected Components library method for implementation details and usage information.
PageRank
Overview
An implementation of a simple PageRank algorithm, using scatter-gather iterations. PageRank is an algorithm that was first used to rank web search engine results. Today, the algorithm and many variations, are used in various graph application domains. The idea of PageRank is that important or relevant pages tend to link to other important pages.
Details
The algorithm operates in iterations, where pages distribute their scores to their neighbors (pages they have links to) and subsequently update their scores based on the partial values they receive. The implementation assumes that each page has at least one incoming and one outgoing link. In order to consider the importance of a link from one page to another, scores are divided by the total number of out-links of the source page. Thus, a page with 10 links will distribute 1/10 of its score to each neighbor, while a page with 100 links, will distribute 1/100 of its score to each neighboring page. This process computes what is often called the transition probablities, i.e. the probability that some page will lead to other page while surfing the web. To correctly compute the transition probabilities, this implementation expectes the edge values to be initialiez to 1.0.
Usage
The algorithm takes as input a Graph with any vertex type, Double vertex values, and Double edge values. Edges values should be initialized to 1.0, in order to correctly compute the transition probabilities. Otherwise, the transition probability for an Edge (u, v) will be set to the edge value divided by u’s out-degree. The algorithm returns a DataSet of vertices, where the vertex value corresponds to assigned rank after convergence (or maximum iterations).
The constructors take the following parameters:
beta: the damping factor.maxIterations: the maximum number of iterations to run.numVertices: the number of vertices in the input. If known beforehand, is it advised to provide this argument to speed up execution.
GSA PageRank
The algorithm is implemented using gather-sum-apply iterations.
See the PageRank library method for implementation details and usage information.
Single Source Shortest Paths
Overview
An implementation of the Single-Source-Shortest-Paths algorithm for weighted graphs. Given a source vertex, the algorithm computes the shortest paths from this source to all other nodes in the graph.
Details
The algorithm is implemented using scatter-gather iterations. In each iteration, a vertex sends to its neighbors a message containing the sum its current distance and the edge weight connecting this vertex with the neighbor. Upon receiving candidate distance messages, a vertex calculates the minimum distance and, if a shorter path has been discovered, it updates its value. If a vertex does not change its value during a superstep, then it does not produce messages for its neighbors for the next superstep. The computation terminates after the specified maximum number of supersteps or when there are no value updates.
Usage
The algorithm takes as input a Graph with any vertex type, Double vertex values, and Double edge values. The output is a DataSet of vertices where the vertex values
correspond to the minimum distances from the given source vertex.
The constructor takes two parameters:
srcVertexIdThe vertex ID of the source vertex.maxIterations: the maximum number of iterations to run.
GSA Single Source Shortest Paths
The algorithm is implemented using gather-sum-apply iterations.
See the Single Source Shortest Paths library method for implementation details and usage information.
GSA Triangle Count
Overview
An implementation of the Triangle Count algorithm. Given an input graph, it returns the number of unique triangles in it.
Details
This algorithm operates in three phases. First, vertices select neighbors with IDs greater than theirs and send messages to them. Each received message is then propagated to neighbors with higher IDs. Finally, if a node encounters the target ID in the list of received messages, it increments the number of discovered triangles.
Usage
The algorithm takes an undirected, unweighted graph as input and outputs a DataSet which contains a single integer corresponding to the number of triangles
in the graph. The algorithm constructor takes no arguments.
Triangle Enumerator
Overview
This library method enumerates unique triangles present in the input graph. A triangle consists of three edges that connect three vertices with each other. This implementation ignores edge directions.
Details
The basic triangle enumeration algorithm groups all edges that share a common vertex and builds triads, i.e., triples of vertices that are connected by two edges. Then, all triads are filtered for which no third edge exists that closes the triangle. For a group of n edges that share a common vertex, the number of built triads is quadratic ((n*(n-1))/2). Therefore, an optimization of the algorithm is to group edges on the vertex with the smaller output degree to reduce the number of triads. This implementation extends the basic algorithm by computing output degrees of edge vertices and grouping on edges on the vertex with the smaller degree.
Usage
The algorithm takes a directed graph as input and outputs a DataSet of Tuple3. The Vertex ID type has to be Comparable.
Each Tuple3 corresponds to a triangle, with the fields containing the IDs of the vertices forming the triangle.
Summarization
Overview
The summarization algorithm computes a condensed version of the input graph by grouping vertices and edges based on their values. In doing so, the algorithm helps to uncover insights about patterns and distributions in the graph. One possible use case is the visualization of communities where the whole graph is too large and needs to be summarized based on the community identifier stored at a vertex.
Details
In the resulting graph, each vertex represents a group of vertices that share the same value. An edge, that connects a vertex with itself, represents all edges with the same edge value that connect vertices from the same vertex group. An edge between different vertices in the output graph represents all edges with the same edge value between members of different vertex groups in the input graph.
The algorithm is implemented using Flink data operators. First, vertices are grouped by their value and a representative is chosen from each group. For any edge, the source and target vertex identifiers are replaced with the corresponding representative and grouped by source, target and edge value. Output vertices and edges are created from their corresponding groupings.
Usage
The algorithm takes a directed, vertex (and possibly edge) attributed graph as input and outputs a new graph where each vertex represents a group of vertices and each edge represents a group of edges from the input graph. Furthermore, each vertex and edge in the output graph stores the common group value and the number of represented elements.