Graph API
- Graph Representation
- Graph Creation
- Graph Properties
- Graph Transformations
- Graph Mutations
- Neighborhood Methods
- Graph Validation
Graph Representation
In Gelly, a Graph is represented by a DataSet of vertices and a DataSet of edges.
The Graph nodes are represented by the Vertex type. A Vertex is defined by a unique ID and a value. Vertex IDs should implement the Comparable interface. Vertices without value can be represented by setting the value type to NullValue.
// create a new vertex with a Long ID and a String value
Vertex<Long, String> v = new Vertex<Long, String>(1L, "foo");
// create a new vertex with a Long ID and no value
Vertex<Long, NullValue> v = new Vertex<Long, NullValue>(1L, NullValue.getInstance());// create a new vertex with a Long ID and a String value
val v = new Vertex(1L, "foo")
// create a new vertex with a Long ID and no value
val v = new Vertex(1L, NullValue.getInstance())The graph edges are represented by the Edge type. An Edge is defined by a source ID (the ID of the source Vertex), a target ID (the ID of the target Vertex) and an optional value. The source and target IDs should be of the same type as the Vertex IDs. Edges with no value have a NullValue value type.
Edge<Long, Double> e = new Edge<Long, Double>(1L, 2L, 0.5);
// reverse the source and target of this edge
Edge<Long, Double> reversed = e.reverse();
Double weight = e.getValue(); // weight = 0.5val e = new Edge(1L, 2L, 0.5)
// reverse the source and target of this edge
val reversed = e.reverse
val weight = e.getValue // weight = 0.5In Gelly an Edge is always directed from the source vertex to the target vertex. A Graph may be undirected if for
every Edge it contains a matching Edge from the target vertex to the source vertex.
Graph Creation
You can create a Graph in the following ways:
- from a
DataSetof edges and an optionalDataSetof vertices:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Vertex<String, Long>> vertices = ...
DataSet<Edge<String, Double>> edges = ...
Graph<String, Long, Double> graph = Graph.fromDataSet(vertices, edges, env);val env = ExecutionEnvironment.getExecutionEnvironment
val vertices: DataSet[Vertex[String, Long]] = ...
val edges: DataSet[Edge[String, Double]] = ...
val graph = Graph.fromDataSet(vertices, edges, env)- from a
DataSetofTuple2representing the edges. Gelly will convert eachTuple2to anEdge, where the first field will be the source ID and the second field will be the target ID. Both vertex and edge values will be set toNullValue.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Tuple2<String, String>> edges = ...
Graph<String, NullValue, NullValue> graph = Graph.fromTuple2DataSet(edges, env);val env = ExecutionEnvironment.getExecutionEnvironment
val edges: DataSet[(String, String)] = ...
val graph = Graph.fromTuple2DataSet(edges, env)- from a
DataSetofTuple3and an optionalDataSetofTuple2. In this case, Gelly will convert eachTuple3to anEdge, where the first field will be the source ID, the second field will be the target ID and the third field will be the edge value. Equivalently, eachTuple2will be converted to aVertex, where the first field will be the vertex ID and the second field will be the vertex value:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Tuple2<String, Long>> vertexTuples = env.readCsvFile("path/to/vertex/input").types(String.class, Long.class);
DataSet<Tuple3<String, String, Double>> edgeTuples = env.readCsvFile("path/to/edge/input").types(String.class, String.class, Double.class);
Graph<String, Long, Double> graph = Graph.fromTupleDataSet(vertexTuples, edgeTuples, env);-
from a CSV file of Edge data and an optional CSV file of Vertex data. In this case, Gelly will convert each row from the Edge CSV file to an
Edge, where the first field will be the source ID, the second field will be the target ID and the third field (if present) will be the edge value. Equivalently, each row from the optional Vertex CSV file will be converted to aVertex, where the first field will be the vertex ID and the second field (if present) will be the vertex value. In order to get aGraphfrom aGraphCsvReaderone has to specify the types, using one of the following methods: types(Class<K> vertexKey, Class<VV> vertexValue,Class<EV> edgeValue): both vertex and edge values are present.edgeTypes(Class<K> vertexKey, Class<EV> edgeValue): the Graph has edge values, but no vertex values.vertexTypes(Class<K> vertexKey, Class<VV> vertexValue): the Graph has vertex values, but no edge values.keyType(Class<K> vertexKey): the Graph has no vertex values and no edge values.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create a Graph with String Vertex IDs, Long Vertex values and Double Edge values
Graph<String, Long, Double> graph = Graph.fromCsvReader("path/to/vertex/input", "path/to/edge/input", env)
.types(String.class, Long.class, Double.class);
// create a Graph with neither Vertex nor Edge values
Graph<Long, NullValue, NullValue> simpleGraph = Graph.fromCsvReader("path/to/edge/input", env).keyType(Long.class);val env = ExecutionEnvironment.getExecutionEnvironment
val vertexTuples = env.readCsvFile[String, Long]("path/to/vertex/input")
val edgeTuples = env.readCsvFile[String, String, Double]("path/to/edge/input")
val graph = Graph.fromTupleDataSet(vertexTuples, edgeTuples, env)- from a CSV file of Edge data and an optional CSV file of Vertex data.
In this case, Gelly will convert each row from the Edge CSV file to an
Edge. The first field of the each row will be the source ID, the second field will be the target ID and the third field (if present) will be the edge value. If the edges have no associated value, set the edge value type parameter (3rd type argument) toNullValue. You can also specify that the vertices are initialized with a vertex value. If you provide a path to a CSV file viapathVertices, each row of this file will be converted to aVertex. The first field of each row will be the vertex ID and the second field will be the vertex value. If you provide a vertex value initializerMapFunctionvia thevertexValueInitializerparameter, then this function is used to generate the vertex values. The set of vertices will be created automatically from the edges input. If the vertices have no associated value, set the vertex value type parameter (2nd type argument) toNullValue. The vertices will then be automatically created from the edges input with vertex value of typeNullValue.
val env = ExecutionEnvironment.getExecutionEnvironment
// create a Graph with String Vertex IDs, Long Vertex values and Double Edge values
val graph = Graph.fromCsvReader[String, Long, Double](
pathVertices = "path/to/vertex/input",
pathEdges = "path/to/edge/input",
env = env)
// create a Graph with neither Vertex nor Edge values
val simpleGraph = Graph.fromCsvReader[Long, NullValue, NullValue](
pathEdges = "path/to/edge/input",
env = env)
// create a Graph with Double Vertex values generated by a vertex value initializer and no Edge values
val simpleGraph = Graph.fromCsvReader[Long, Double, NullValue](
pathEdges = "path/to/edge/input",
vertexValueInitializer = new MapFunction[Long, Double]() {
def map(id: Long): Double = {
id.toDouble
}
},
env = env)- from a
Collectionof edges and an optionalCollectionof vertices:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
List<Vertex<Long, Long>> vertexList = new ArrayList...
List<Edge<Long, String>> edgeList = new ArrayList...
Graph<Long, Long, String> graph = Graph.fromCollection(vertexList, edgeList, env);If no vertex input is provided during Graph creation, Gelly will automatically produce the Vertex DataSet from the edge input. In this case, the created vertices will have no values. Alternatively, you can provide a MapFunction as an argument to the creation method, in order to initialize the Vertex values:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// initialize the vertex value to be equal to the vertex ID
Graph<Long, Long, String> graph = Graph.fromCollection(edgeList,
new MapFunction<Long, Long>() {
public Long map(Long value) {
return value;
}
}, env);val env = ExecutionEnvironment.getExecutionEnvironment
val vertexList = List(...)
val edgeList = List(...)
val graph = Graph.fromCollection(vertexList, edgeList, env)If no vertex input is provided during Graph creation, Gelly will automatically produce the Vertex DataSet from the edge input. In this case, the created vertices will have no values. Alternatively, you can provide a MapFunction as an argument to the creation method, in order to initialize the Vertex values:
val env = ExecutionEnvironment.getExecutionEnvironment
// initialize the vertex value to be equal to the vertex ID
val graph = Graph.fromCollection(edgeList,
new MapFunction[Long, Long] {
def map(id: Long): Long = id
}, env)Graph Properties
Gelly includes the following methods for retrieving various Graph properties and metrics:
// get the Vertex DataSet
DataSet<Vertex<K, VV>> getVertices()
// get the Edge DataSet
DataSet<Edge<K, EV>> getEdges()
// get the IDs of the vertices as a DataSet
DataSet<K> getVertexIds()
// get the source-target pairs of the edge IDs as a DataSet
DataSet<Tuple2<K, K>> getEdgeIds()
// get a DataSet of <vertex ID, in-degree> pairs for all vertices
DataSet<Tuple2<K, LongValue>> inDegrees()
// get a DataSet of <vertex ID, out-degree> pairs for all vertices
DataSet<Tuple2<K, LongValue>> outDegrees()
// get a DataSet of <vertex ID, degree> pairs for all vertices, where degree is the sum of in- and out- degrees
DataSet<Tuple2<K, LongValue>> getDegrees()
// get the number of vertices
long numberOfVertices()
// get the number of edges
long numberOfEdges()
// get a DataSet of Triplets<srcVertex, trgVertex, edge>
DataSet<Triplet<K, VV, EV>> getTriplets()// get the Vertex DataSet
getVertices: DataSet[Vertex[K, VV]]
// get the Edge DataSet
getEdges: DataSet[Edge[K, EV]]
// get the IDs of the vertices as a DataSet
getVertexIds: DataSet[K]
// get the source-target pairs of the edge IDs as a DataSet
getEdgeIds: DataSet[(K, K)]
// get a DataSet of <vertex ID, in-degree> pairs for all vertices
inDegrees: DataSet[(K, LongValue)]
// get a DataSet of <vertex ID, out-degree> pairs for all vertices
outDegrees: DataSet[(K, LongValue)]
// get a DataSet of <vertex ID, degree> pairs for all vertices, where degree is the sum of in- and out- degrees
getDegrees: DataSet[(K, LongValue)]
// get the number of vertices
numberOfVertices: Long
// get the number of edges
numberOfEdges: Long
// get a DataSet of Triplets<srcVertex, trgVertex, edge>
getTriplets: DataSet[Triplet[K, VV, EV]]Graph Transformations
- Map: Gelly provides specialized methods for applying a map transformation on the vertex values or edge values.
mapVerticesandmapEdgesreturn a newGraph, where the IDs of the vertices (or edges) remain unchanged, while the values are transformed according to the provided user-defined map function. The map functions also allow changing the type of the vertex or edge values.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, Long> graph = Graph.fromDataSet(vertices, edges, env);
// increment each vertex value by one
Graph<Long, Long, Long> updatedGraph = graph.mapVertices(
new MapFunction<Vertex<Long, Long>, Long>() {
public Long map(Vertex<Long, Long> value) {
return value.getValue() + 1;
}
});val env = ExecutionEnvironment.getExecutionEnvironment
val graph = Graph.fromDataSet(vertices, edges, env)
// increment each vertex value by one
val updatedGraph = graph.mapVertices(v => v.getValue + 1)- Translate: Gelly provides specialized methods for translating the value and/or type of vertex and edge IDs (
translateGraphIDs), vertex values (translateVertexValues), or edge values (translateEdgeValues). Translation is performed by the user-defined map function, several of which are provided in theorg.apache.flink.graph.asm.translatepackage. The sameMapFunctioncan be used for all the three translate methods.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, Long> graph = Graph.fromDataSet(vertices, edges, env);
// translate each vertex and edge ID to a String
Graph<String, Long, Long> updatedGraph = graph.translateGraphIds(
new MapFunction<Long, String>() {
public String map(Long id) {
return id.toString();
}
});
// translate vertex IDs, edge IDs, vertex values, and edge values to LongValue
Graph<LongValue, LongValue, LongValue> updatedGraph = graph
.translateGraphIds(new LongToLongValue())
.translateVertexValues(new LongToLongValue())
.translateEdgeValues(new LongToLongValue())val env = ExecutionEnvironment.getExecutionEnvironment
val graph = Graph.fromDataSet(vertices, edges, env)
// translate each vertex and edge ID to a String
val updatedGraph = graph.translateGraphIds(id => id.toString)- Filter: A filter transformation applies a user-defined filter function on the vertices or edges of the
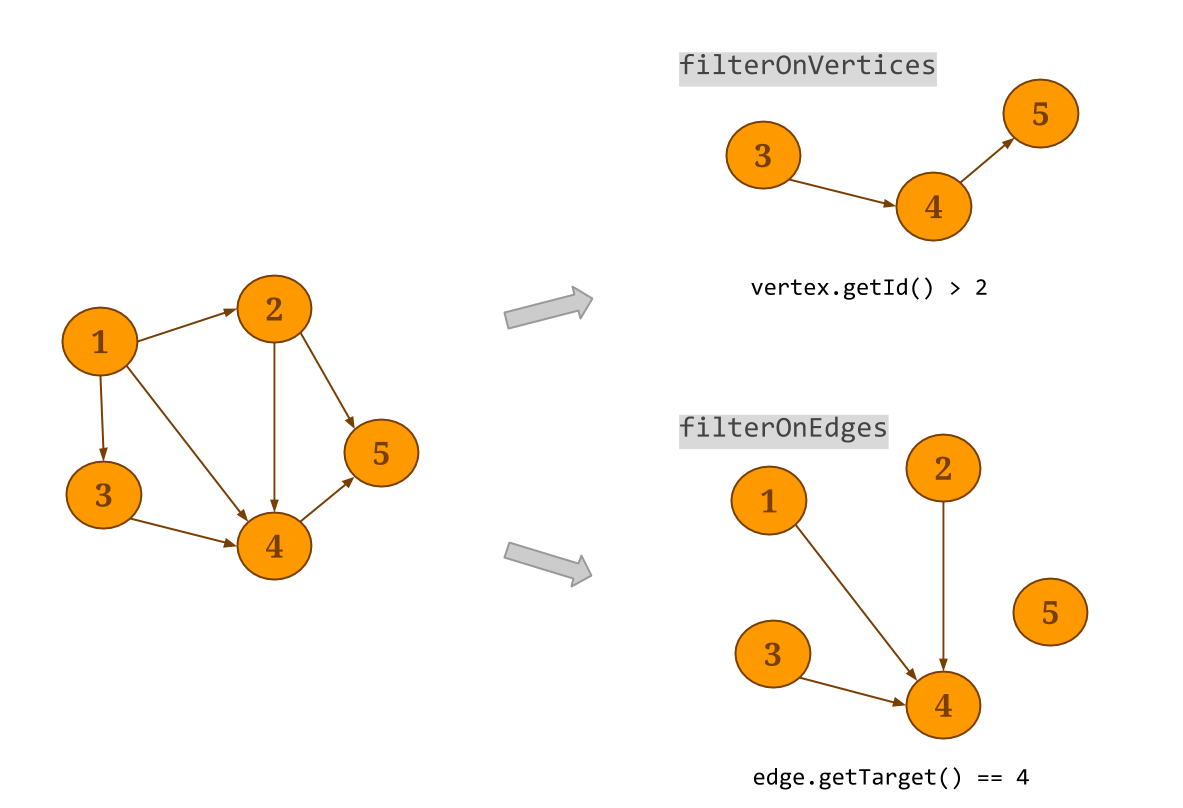
Graph.filterOnEdgeswill create a sub-graph of the original graph, keeping only the edges that satisfy the provided predicate. Note that the vertex dataset will not be modified. Respectively,filterOnVerticesapplies a filter on the vertices of the graph. Edges whose source and/or target do not satisfy the vertex predicate are removed from the resulting edge dataset. Thesubgraphmethod can be used to apply a filter function to the vertices and the edges at the same time.
Graph<Long, Long, Long> graph = ...
graph.subgraph(
new FilterFunction<Vertex<Long, Long>>() {
public boolean filter(Vertex<Long, Long> vertex) {
// keep only vertices with positive values
return (vertex.getValue() > 0);
}
},
new FilterFunction<Edge<Long, Long>>() {
public boolean filter(Edge<Long, Long> edge) {
// keep only edges with negative values
return (edge.getValue() < 0);
}
})val graph: Graph[Long, Long, Long] = ...
// keep only vertices with positive values
// and only edges with negative values
graph.subgraph((vertex => vertex.getValue > 0), (edge => edge.getValue < 0))
- Join: Gelly provides specialized methods for joining the vertex and edge datasets with other input datasets.
joinWithVerticesjoins the vertices with aTuple2input data set. The join is performed using the vertex ID and the first field of theTuple2input as the join keys. The method returns a newGraphwhere the vertex values have been updated according to a provided user-defined transformation function. Similarly, an input dataset can be joined with the edges, using one of three methods.joinWithEdgesexpects an inputDataSetofTuple3and joins on the composite key of both source and target vertex IDs.joinWithEdgesOnSourceexpects aDataSetofTuple2and joins on the source key of the edges and the first attribute of the input dataset andjoinWithEdgesOnTargetexpects aDataSetofTuple2and joins on the target key of the edges and the first attribute of the input dataset. All three methods apply a transformation function on the edge and the input data set values. Note that if the input dataset contains a key multiple times, all Gelly join methods will only consider the first value encountered.
Graph<Long, Double, Double> network = ...
DataSet<Tuple2<Long, LongValue>> vertexOutDegrees = network.outDegrees();
// assign the transition probabilities as the edge weights
Graph<Long, Double, Double> networkWithWeights = network.joinWithEdgesOnSource(vertexOutDegrees,
new VertexJoinFunction<Double, LongValue>() {
public Double vertexJoin(Double vertexValue, LongValue inputValue) {
return vertexValue / inputValue.getValue();
}
});val network: Graph[Long, Double, Double] = ...
val vertexOutDegrees: DataSet[(Long, LongValue)] = network.outDegrees
// assign the transition probabilities as the edge weights
val networkWithWeights = network.joinWithEdgesOnSource(vertexOutDegrees, (v1: Double, v2: LongValue) => v1 / v2.getValue)-
Reverse: the
reverse()method returns a newGraphwhere the direction of all edges has been reversed. -
Undirected: In Gelly, a
Graphis always directed. Undirected graphs can be represented by adding all opposite-direction edges to a graph. For this purpose, Gelly provides thegetUndirected()method. -
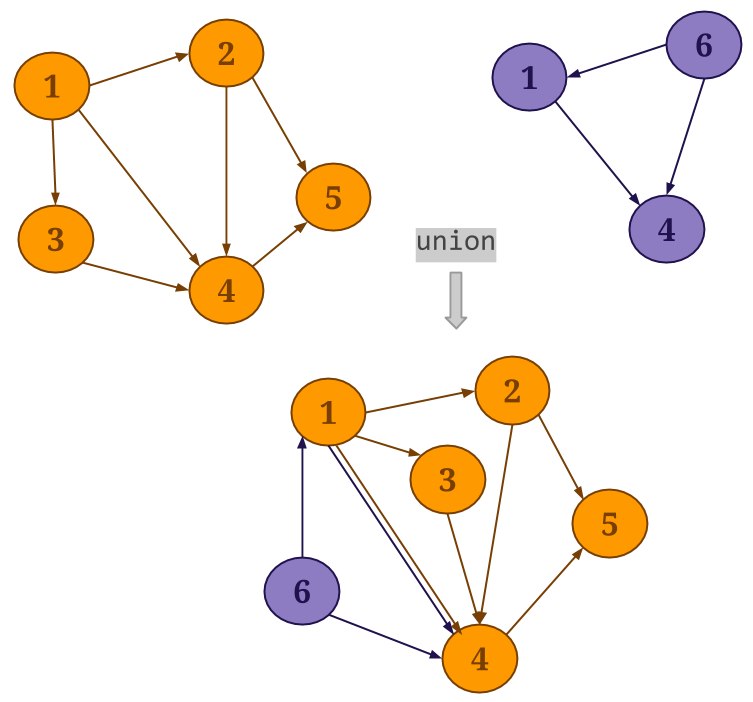
Union: Gelly’s
union()method performs a union operation on the vertex and edge sets of the specified graph and the current graph. Duplicate vertices are removed from the resultingGraph, while if duplicate edges exist, these will be preserved.
-
Difference: Gelly’s
difference()method performs a difference on the vertex and edge sets of the current graph and the specified graph. -
Intersect: Gelly’s
intersect()method performs an intersect on the edge sets of the current graph and the specified graph. The result is a newGraphthat contains all edges that exist in both input graphs. Two edges are considered equal, if they have the same source identifier, target identifier and edge value. Vertices in the resulting graph have no value. If vertex values are required, one can for example retrieve them from one of the input graphs using thejoinWithVertices()method. Depending on the parameterdistinct, equal edges are either contained once in the resultingGraphor as often as there are pairs of equal edges in the input graphs.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create first graph from edges {(1, 3, 12) (1, 3, 13), (1, 3, 13)}
List<Edge<Long, Long>> edges1 = ...
Graph<Long, NullValue, Long> graph1 = Graph.fromCollection(edges1, env);
// create second graph from edges {(1, 3, 13)}
List<Edge<Long, Long>> edges2 = ...
Graph<Long, NullValue, Long> graph2 = Graph.fromCollection(edges2, env);
// Using distinct = true results in {(1,3,13)}
Graph<Long, NullValue, Long> intersect1 = graph1.intersect(graph2, true);
// Using distinct = false results in {(1,3,13),(1,3,13)} as there is one edge pair
Graph<Long, NullValue, Long> intersect2 = graph1.intersect(graph2, false);val env = ExecutionEnvironment.getExecutionEnvironment
// create first graph from edges {(1, 3, 12) (1, 3, 13), (1, 3, 13)}
val edges1: List[Edge[Long, Long]] = ...
val graph1 = Graph.fromCollection(edges1, env)
// create second graph from edges {(1, 3, 13)}
val edges2: List[Edge[Long, Long]] = ...
val graph2 = Graph.fromCollection(edges2, env)
// Using distinct = true results in {(1,3,13)}
val intersect1 = graph1.intersect(graph2, true)
// Using distinct = false results in {(1,3,13),(1,3,13)} as there is one edge pair
val intersect2 = graph1.intersect(graph2, false)Graph Mutations
Gelly includes the following methods for adding and removing vertices and edges from an input Graph:
// adds a Vertex to the Graph. If the Vertex already exists, it will not be added again.
Graph<K, VV, EV> addVertex(final Vertex<K, VV> vertex)
// adds a list of vertices to the Graph. If the vertices already exist in the graph, they will not be added once more.
Graph<K, VV, EV> addVertices(List<Vertex<K, VV>> verticesToAdd)
// adds an Edge to the Graph. If the source and target vertices do not exist in the graph, they will also be added.
Graph<K, VV, EV> addEdge(Vertex<K, VV> source, Vertex<K, VV> target, EV edgeValue)
// adds a list of edges to the Graph. When adding an edge for a non-existing set of vertices, the edge is considered invalid and ignored.
Graph<K, VV, EV> addEdges(List<Edge<K, EV>> newEdges)
// removes the given Vertex and its edges from the Graph.
Graph<K, VV, EV> removeVertex(Vertex<K, VV> vertex)
// removes the given list of vertices and their edges from the Graph
Graph<K, VV, EV> removeVertices(List<Vertex<K, VV>> verticesToBeRemoved)
// removes *all* edges that match the given Edge from the Graph.
Graph<K, VV, EV> removeEdge(Edge<K, EV> edge)
// removes *all* edges that match the edges in the given list
Graph<K, VV, EV> removeEdges(List<Edge<K, EV>> edgesToBeRemoved)// adds a Vertex to the Graph. If the Vertex already exists, it will not be added again.
addVertex(vertex: Vertex[K, VV])
// adds a list of vertices to the Graph. If the vertices already exist in the graph, they will not be added once more.
addVertices(verticesToAdd: List[Vertex[K, VV]])
// adds an Edge to the Graph. If the source and target vertices do not exist in the graph, they will also be added.
addEdge(source: Vertex[K, VV], target: Vertex[K, VV], edgeValue: EV)
// adds a list of edges to the Graph. When adding an edge for a non-existing set of vertices, the edge is considered invalid and ignored.
addEdges(edges: List[Edge[K, EV]])
// removes the given Vertex and its edges from the Graph.
removeVertex(vertex: Vertex[K, VV])
// removes the given list of vertices and their edges from the Graph
removeVertices(verticesToBeRemoved: List[Vertex[K, VV]])
// removes *all* edges that match the given Edge from the Graph.
removeEdge(edge: Edge[K, EV])
// removes *all* edges that match the edges in the given list
removeEdges(edgesToBeRemoved: List[Edge[K, EV]])Neighborhood Methods
Neighborhood methods allow vertices to perform an aggregation on their first-hop neighborhood.
reduceOnEdges() can be used to compute an aggregation on the values of the neighboring edges of a vertex and reduceOnNeighbors() can be used to compute an aggregation on the values of the neighboring vertices. These methods assume associative and commutative aggregations and exploit combiners internally, significantly improving performance.
The neighborhood scope is defined by the EdgeDirection parameter, which takes the values IN, OUT or ALL. IN will gather all in-coming edges (neighbors) of a vertex, OUT will gather all out-going edges (neighbors), while ALL will gather all edges (neighbors).
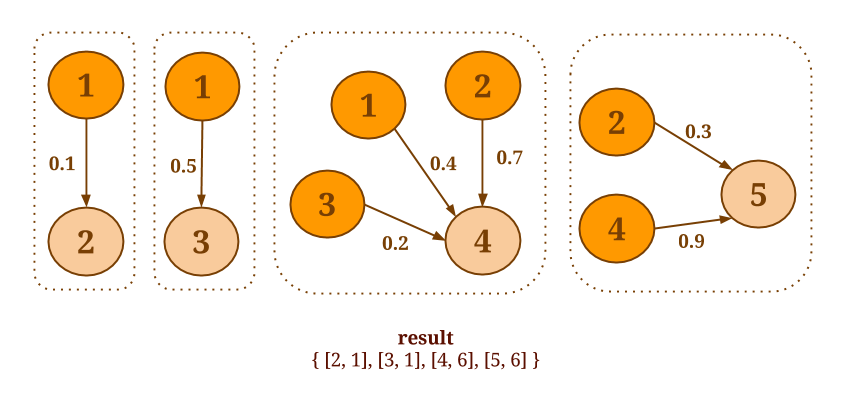
For example, assume that you want to select the minimum weight of all out-edges for each vertex in the following graph:
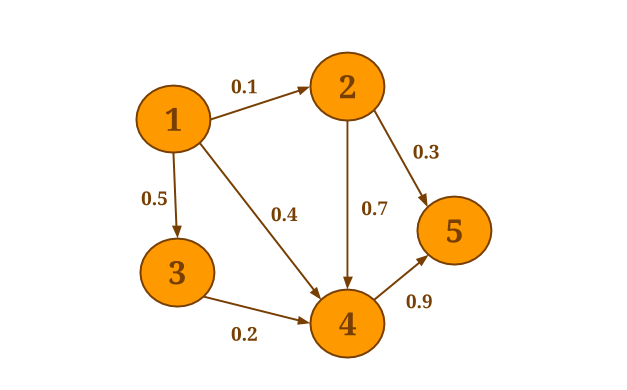
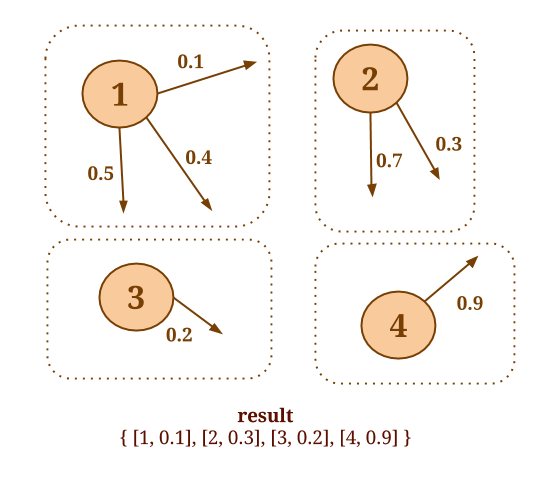
The following code will collect the out-edges for each vertex and apply the SelectMinWeight() user-defined function on each of the resulting neighborhoods:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Long, Double>> minWeights = graph.reduceOnEdges(new SelectMinWeight(), EdgeDirection.OUT);
// user-defined function to select the minimum weight
static final class SelectMinWeight implements ReduceEdgesFunction<Double> {
@Override
public Double reduceEdges(Double firstEdgeValue, Double secondEdgeValue) {
return Math.min(firstEdgeValue, secondEdgeValue);
}
}val graph: Graph[Long, Long, Double] = ...
val minWeights = graph.reduceOnEdges(new SelectMinWeight, EdgeDirection.OUT)
// user-defined function to select the minimum weight
final class SelectMinWeight extends ReduceEdgesFunction[Double] {
override def reduceEdges(firstEdgeValue: Double, secondEdgeValue: Double): Double = {
Math.min(firstEdgeValue, secondEdgeValue)
}
}
Similarly, assume that you would like to compute the sum of the values of all in-coming neighbors, for every vertex. The following code will collect the in-coming neighbors for each vertex and apply the SumValues() user-defined function on each neighborhood:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Long, Long>> verticesWithSum = graph.reduceOnNeighbors(new SumValues(), EdgeDirection.IN);
// user-defined function to sum the neighbor values
static final class SumValues implements ReduceNeighborsFunction<Long> {
@Override
public Long reduceNeighbors(Long firstNeighbor, Long secondNeighbor) {
return firstNeighbor + secondNeighbor;
}
}val graph: Graph[Long, Long, Double] = ...
val verticesWithSum = graph.reduceOnNeighbors(new SumValues, EdgeDirection.IN)
// user-defined function to sum the neighbor values
final class SumValues extends ReduceNeighborsFunction[Long] {
override def reduceNeighbors(firstNeighbor: Long, secondNeighbor: Long): Long = {
firstNeighbor + secondNeighbor
}
}
When the aggregation function is not associative and commutative or when it is desirable to return more than one values per vertex, one can use the more general
groupReduceOnEdges() and groupReduceOnNeighbors() methods.
These methods return zero, one or more values per vertex and provide access to the whole neighborhood.
For example, the following code will output all the vertex pairs which are connected with an edge having a weight of 0.5 or more:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> vertexPairs = graph.groupReduceOnNeighbors(new SelectLargeWeightNeighbors(), EdgeDirection.OUT);
// user-defined function to select the neighbors which have edges with weight > 0.5
static final class SelectLargeWeightNeighbors implements NeighborsFunctionWithVertexValue<Long, Long, Double,
Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> {
@Override
public void iterateNeighbors(Vertex<Long, Long> vertex,
Iterable<Tuple2<Edge<Long, Double>, Vertex<Long, Long>>> neighbors,
Collector<Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> out) {
for (Tuple2<Edge<Long, Double>, Vertex<Long, Long>> neighbor : neighbors) {
if (neighbor.f0.f2 > 0.5) {
out.collect(new Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>(vertex, neighbor.f1));
}
}
}
}val graph: Graph[Long, Long, Double] = ...
val vertexPairs = graph.groupReduceOnNeighbors(new SelectLargeWeightNeighbors, EdgeDirection.OUT)
// user-defined function to select the neighbors which have edges with weight > 0.5
final class SelectLargeWeightNeighbors extends NeighborsFunctionWithVertexValue[Long, Long, Double,
(Vertex[Long, Long], Vertex[Long, Long])] {
override def iterateNeighbors(vertex: Vertex[Long, Long],
neighbors: Iterable[(Edge[Long, Double], Vertex[Long, Long])],
out: Collector[(Vertex[Long, Long], Vertex[Long, Long])]) = {
for (neighbor <- neighbors) {
if (neighbor._1.getValue() > 0.5) {
out.collect(vertex, neighbor._2)
}
}
}
}When the aggregation computation does not require access to the vertex value (for which the aggregation is performed), it is advised to use the more efficient EdgesFunction and NeighborsFunction for the user-defined functions. When access to the vertex value is required, one should use EdgesFunctionWithVertexValue and NeighborsFunctionWithVertexValue instead.
Graph Validation
Gelly provides a simple utility for performing validation checks on input graphs. Depending on the application context, a graph may or may not be valid according to certain criteria. For example, a user might need to validate whether their graph contains duplicate edges or whether its structure is bipartite. In order to validate a graph, one can define a custom GraphValidator and implement its validate() method. InvalidVertexIdsValidator is Gelly’s pre-defined validator. It checks that the edge set contains valid vertex IDs, i.e. that all edge IDs
also exist in the vertex IDs set.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create a list of vertices with IDs = {1, 2, 3, 4, 5}
List<Vertex<Long, Long>> vertices = ...
// create a list of edges with IDs = {(1, 2) (1, 3), (2, 4), (5, 6)}
List<Edge<Long, Long>> edges = ...
Graph<Long, Long, Long> graph = Graph.fromCollection(vertices, edges, env);
// will return false: 6 is an invalid ID
graph.validate(new InvalidVertexIdsValidator<Long, Long, Long>());val env = ExecutionEnvironment.getExecutionEnvironment
// create a list of vertices with IDs = {1, 2, 3, 4, 5}
val vertices: List[Vertex[Long, Long]] = ...
// create a list of edges with IDs = {(1, 2) (1, 3), (2, 4), (5, 6)}
val edges: List[Edge[Long, Long]] = ...
val graph = Graph.fromCollection(vertices, edges, env)
// will return false: 6 is an invalid ID
graph.validate(new InvalidVertexIdsValidator[Long, Long, Long])